1.2b Data storage

• Why is binary used?
• Converting from denary (decimal) to binary and vice versa
• Why is hexadecimal used?
• Converting from denary (decimal) to hex and vice versa
• Character sets (ASCII and Unicode)
• Sound sampling
• Images
• Compression
• Calculating file sizes

Why is binary used?

Binary is used as it only has two possible values 0 and 1. This is to represent the transistor switches that exist in the CPU which can either be ON or OFF. The CPU can only work with binary so all code has to be translated into binary machine code.

Converting from denary (decimal) to binary and vice versa

The key to converting to and from binary is writing out the column headings first. Always remember the smallest number goes on the right!

32 + 16+ 4 + 2 = 54

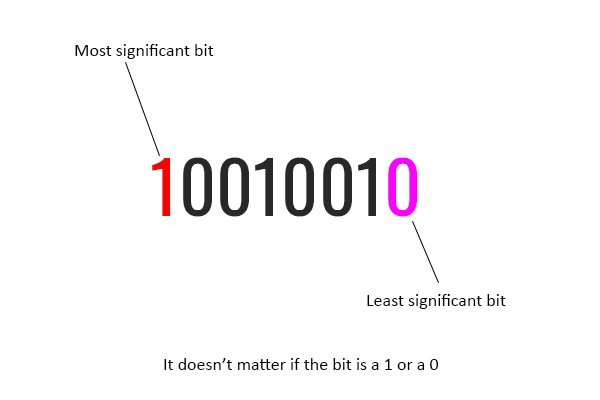
Most and least significant bit

In binary, the most significant bit is the bit that is furthest to the left i.e. the bit that has the highest value.

The least significant bit is the bit that is furthest to the right i.e. the bit that has the lowest value.

Why is hexadecimal used?

Binary can be difficult to work with and it is easy to make a mistake. Hexadecimal is less prone to errors and it is very easy to convert between binary and hex so lots of computer scientists prefer using it. You can see hex references in colour codes and memory addresses.

Converting from denary (decimal) to hex and vice versa

The key to converting to and from hex is writing out the column headings and the numbers 1-15 with their hex equivalent. Do this in the exam! This will prevent you making any mistakes and you won’t lose any marks.

1	2	3	4	5	6	7	8	9	10	11	12	13	14	15
1	2	3	4	5	6	7	8	9	A	B	C	D	E	F

The conversions you need

You will need the following skills:

• How to convert from denary to binary and vice versa.
• How to convert from denary to hex and vice versa.
• How to convert from binary to hex and vice versa (without converting to denary first).
• How to add two binary numbers.
• Explain overflow errors when adding binary numbers.
• Binary shifts.

The best place to practice all of these skills is at the Learn Computing Binary Quiz.

Just work your way through all the tasks in the GCSE menu and you will become a master of this section of the course.

Character sets (ASCII and Unicode)

Characters like letters, numbers and symbols need to be stored in binary just like everything else in a computer. The way this is done is simply just to give each letter or symbol a unique binary number. Of course, there are lots of different ways this could be done. Each one is called a character set. The two varieties you need to know are ASCII and Unicode.

ASCII

The American Standard Code for Information Interchange. This character set uses 8 bits to represent characters meaning there are 256 possible combinations. This is only enough to cover English letters and a few extra symbols. Each character is given a unique binary number.

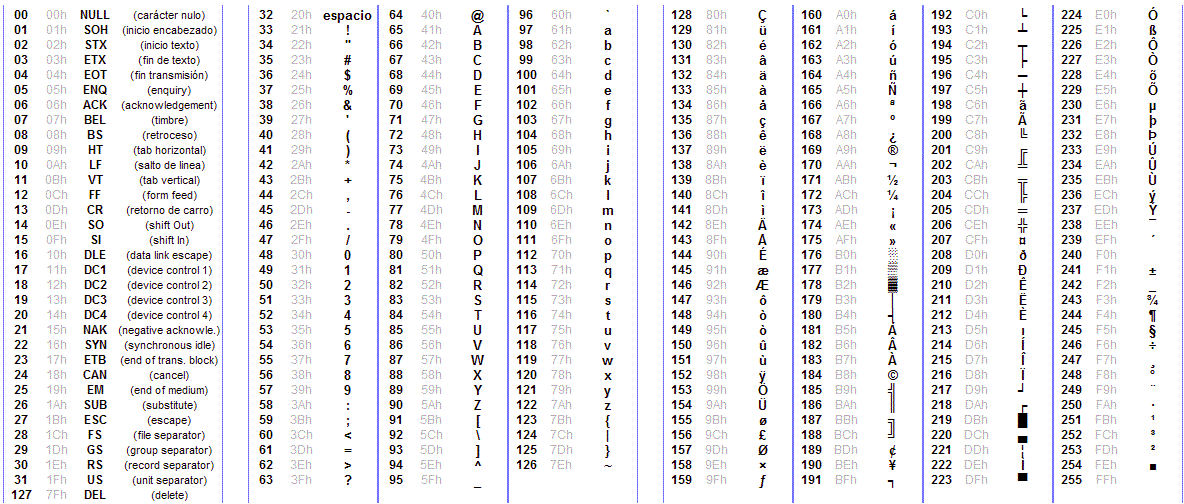
The original ASCII table only used 7 of the 8 available bits (just 128 combinations) but a later version called the Extended ASCII table used all 8-bits and was in common use for many years. Here is the Extended ASCII table:

Unicode

As ASCII is only real good if you are an English speaker, there used to be lots of different character sets all over the world for countries with different alphabets e.g. Greece, Russia, China etc. This got to be too complicated so computer scientists invented a character set to include all languages in. It is called Unicode and it uses up to 32-bits for each character. As there are more bits, there are more possible combinations and there are up to 4,294,967,296 possible characters. This is enough for all languages on Earth with quite a few left over for spare. You can see the full Unicode table here.

Sound sampling

Sound needs to be converted to binary to be used and stored in a computer system.

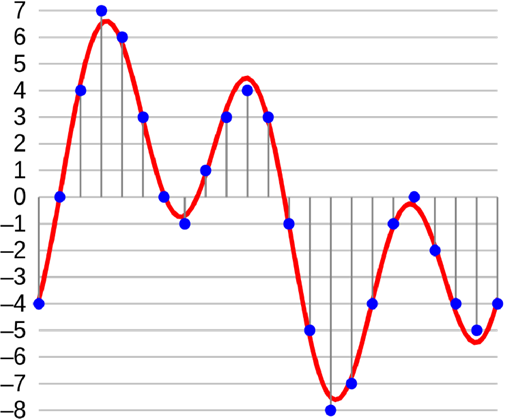
To turn sound into binary we need to sample it.

An analogue sound wave is taken and the amplitude (height) of the wave is measured at regular intervals. This is converted into a binary number.

SAMPLING FREQUENCY/RATE
The more often the amplitude is measured, the better the quality of the sound.

Increasing the sampling frequency makes the sample more true to the original but increases the file size.

BIT DEPTH
This refers to the number of bits of data taken during each sample.

The higher the bit depth, the closer to the original the sample will be but the file size will be higher.

Images

Images need to be converted into binary to be stored in a computer. A common way of doing this is using a bitmap.

Bitmap images are made up of pixels. For each pixel a binary number is stored that represents a colour.

Resolution: The number of pixels in an image, often given as a height and width e.g. 1920x1080. The more pixels there are, the more detailed the image will be, but the higher the file size will be.

Colour depth: The number of bits used to store the colour value e.g. 8-bits, 16-bits. The more bits used, the more colours are available in the image but the higher the file size will be.

Metadata: This is data that goes at the start of an image file that tells you about the file. It might say the resolution, the colour depth, the geo location of where the picture was taken, the device it was taken on. It will not say the file size.

Image Creating Apps

Don't forget you can learn about bitmap images using the Learn Computing Bitmap Creator.
And you can compare how they work with vector images using the Learn Computing Vector Creator.